Œ“ÇÉ∂º÷™µ¿��£¨ê€“ÚÀπÃπµƒèV¡xœýå¶’ì «¨F(xi®§n)¥˙ŒÔ¿ÌåWµƒª˘ Ø÷Æ“ª����£¨À¸Ω“ æ¡Àïrø’∫Ռԟ|(zh®¨)÷ÆÈgµƒ…Óøìì(li®¢n)œµ���°£èV¡xœý嶒ì∏Ê‘VŒ“ÇÉ�£¨ïrø’≤¢≤ª «“ª≥…≤ª◊ɵƒ�£¨∂¯ «“ªÇÄÑ”ëB(t®§i)µƒåçÛw�����£¨À¸ï˛ÎS÷¯ŒÔŸ|(zh®¨)µƒ∑÷≤º∫Õþ\Ñ”∂¯∞l(f®°)…˙◊ɪØ�°£

‘⁄‘S∂ýø∆∆’Œƒ’¬Æî÷–£¨èù«˙µƒïrø’∫Õ≈§«˙µƒïrø’ «ªÏ”√µƒ�°£µ´ «��£¨‘⁄èV¡xœý嶒ì÷–�����£¨ïrø’µƒèù«˙∫Õ≈§«˙≤¢≤ª «“ªªÿ ¬����°£ƒ«√¥��£¨èù«˙ïrø’∫Õ≈§«˙ïrø’”– ≤√¥Ö^(q®±)Ñeƒÿ����£ø
≤√¥ «ïrø’
◊œ»£¨Œ“ÇÉ“™√˜∞◊ ≤√¥ «ïrø’���°£∫ÜÜŒµÿ’f����£¨ïrø’æÕ «Œ“ÇÉ…˙ªÓµƒÀƒæS ¿ΩÁ�����£¨À¸∞¸¿®»˝ÇÄø’ÈgæS∂»∫Õ“ªÇÄïrÈgæS∂»°£Œ“ÇÉø…“‘”√“ªÇÄ◊¯òÀœµÅÌ√Ë ˆïrø’÷–µƒ»Œ∫Œ ¬º˛ªÚŒÔÛw��£¨¿˝»Á£®x,y,z,t£©���£¨∆‰÷–x,y,z±Ì æø’ÈgŒª÷√�����£¨t±Ì æïrÈg����°£
ïrø’≤ª «“ªÇÄ≥Ȝ۵ƒîµ(sh®¥)åW∏≈ƒÓ����£¨∂¯ «“ªÇÄ’Êå絃ŒÔ¿ÌåçÛw°£À¸ø…“‘±ªúy¡ø∫Õ”^≤Ï�����°£¿˝»Á�£¨Œ“ÇÉø…“‘”√π‚ÅÌÃΩúyïrø’µƒ–‘Ÿ|(zh®¨)°£π‚‘⁄’Êø’÷–—ÿ÷¯÷±æÄǘ≤•�����£¨þ@ól÷±æÄæÕ «ïrø’÷–µƒ◊Ó∂ì∑èΩ���£¨“≤Ω–◊˜úyµÿæÄ�����°£þ@ò”����£¨Œ“ÇÉæÕø…“‘Õ®þ^”^≤Ïπ‚æĵƒ∆´’€ÅÌ≈–îýïrø’ «∑Ò”–èù«˙ªÚ≈§«˙��°£

èù«˙µƒïrø’
èù«˙ø…“‘√Ë ˆïrø’÷–≤ªÕ¨∑ΩœÚ÷ÆÈg¥Ê‘⁄Ω«∂»∆´≤Ó�£¨À¸”…¿Ë¬¸«˙¬ èà¡øÅ̱Ìþ_°£¿Ë¬¸«˙¬ èà¡ø «“ªÇÄÀƒÎA∑¥å¶∑Qèà¡øàˆ����£¨À¸∂®¡xûÈ£∫R(X,Y,Z,W)=g(R(X,Y)Z,W)°£∆‰÷– X,Y,Z,W «»Œ“‚µƒœÚ¡øàˆ��£¨ g «¿Ë¬¸¡˜–Œ…œµƒ∂»¡ø��£¨ R(X,Y)Z «“ªÇĜڡøàˆ����£¨À¸±Ì æ—ÿ÷¯ X ∫Õ Y ∑ΩœÚµƒ∆Ω––“∆Ñ”∫Û£¨ Z œÚ¡øµƒ◊ɪءø°£
¿Ë¬¸«˙¬ èà¡ø∫‚¡ø¡ÀÖf(xi®¶)◊Éåßîµ(sh®¥)µƒ∑¥ΩªìQ–‘����£¨º¥∆Ω––“∆Ñ”µƒÌò–Ú?q®±)¶ΩY(ji®¶)π˚µƒ”∞Ìë°£»Áπ˚¿Ë¬¸«˙¬ èà¡øûÈ¡„�£¨ƒ«√¥Öf(xi®¶)◊Éåßîµ(sh®¥)æÕ «å¶“◊µƒ£¨º¥∆Ω––“∆Ñ”µƒÌò–ÚüoÍP(gu®°n)æo“™���°£‘⁄þ@∑N«Èõrœ¬���£¨¡˜–ŒæÕ «∆Ω÷±µƒ°£
¨F(xi®§n)‘⁄�£¨Œ“ÇÉæÕ“‘“ª∑N∏¸»ð“◊∂Ƶƒ∑Ω Ω£¨ÅÌ√Ë ˆ«˙¬ µƒé◊∫Œ“‚¡x�����°£Æîïrø’¥Ê‘⁄«˙¬ ïr�����£¨“ªÇÄ ∏¡ø—ÿ÷¯È]∫œ«˙æÄ∆Ω“∆“ª÷Ð∫Û�£¨À¸≤¢≤ª≈c‘≠ ∏¡ø÷ÿ∫œ£¨∂¯ «œý≤Ó“ªÇÄΩ«∂»���°£±ÿÌö‘Ÿ∏Ωº”“ªÇÄÞD(zhu®£n)Ñ”��£¨À¸Çz≤≈ƒÐ÷ÿ∫œ��£¨∂¯þ@ÇÄ∏Ωº”µƒÞD(zhu®£n)Ñ”�����£¨’˝ «ø’Èg«˙¬ £®èù«˙£©Æa(ch®£n)…˙µƒé◊∫Œ–ßë™���°£
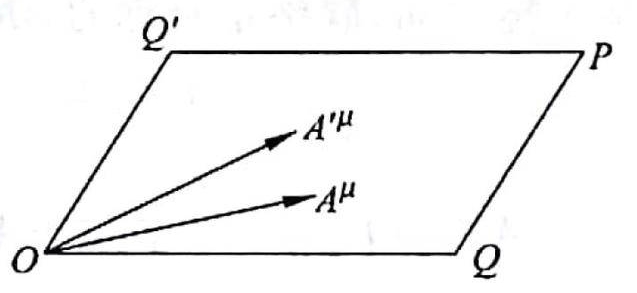
‘⁄ŒÔ¿Ì…œ£¨¿Ë¬¸«˙¬ èà¡øø…“‘√Ë ˆïrø’÷–¥Ê‘⁄µƒ“˝¡¶àˆªÚŒÔŸ|(zh®¨)ƒÐ¡ø∑÷≤º���£¨À¸ÇÉï˛ πµ√ïrø’Æa(ch®£n)…˙èù«˙�°£¿˝»Á��£¨‘⁄èV¡xœý嶒ì÷–����£¨“˝¡¶àˆ∑Ω≥à «“ªÇÄÍP(gu®°n)”⁄¿Ë¬¸«˙¬ èà¡ø∫ÕƒÐÑ”èà¡øµƒ∑Ω≥ã¨À¸∑¥”≥¡ÀŒÔŸ|(zh®¨)∫ՃСøå¶ïrø’èù«˙µƒ”∞Ìë��°£‘⁄þ@∑N¿Ì’ì÷–�£¨ïrø’ «èù«˙µƒ��°£
≈§«˙µƒïrø’
≈§«˙ø…“‘√Ë ˆïrø’÷–≤ªÕ¨¸c÷ÆÈg¥Ê‘⁄∆Ω“∆∆´≤ÓªÚ–˝ÞD(zhu®£n)∆´≤Ó��£¨À¸”…윬 èà¡øÅ̱Ìþ_���°£ìœ¬ èà¡ø «“ªÇÄ»˝ÎA∑¥å¶∑Qèà¡øàˆ£¨À¸∂®¡xûÈ£∫T(X,Y)=∇XY−∇YX−[X,Y]�����°£∆‰÷– X,Y «»Œ“‚µƒœÚ¡øàˆ�����£¨ ∇ «»Œ“‚µƒ∑¬…‰¬ì(li®¢n)Ωj(lu®∞)���£¨ [X,Y] «œÚ¡øàˆµƒLie¿®Ãñ�����°£
윬 èà¡ø∫‚¡ø¡À¬ì(li®¢n)Ωj(lu®∞)µƒ∑«å¶∑Q–‘ªÚ∑«∂»¡ø–‘�����£¨º¥Öf(xi®¶)◊Éåßîµ(sh®¥)≈cœÚ¡øàˆµƒΩªìQ≤ª“ª÷¬���°£»Áπ˚윬 èà¡øûÈ¡„���£¨ƒ«√¥¬ì(li®¢n)Ωj(lu®∞)æÕ «å¶∑QµƒªÚ∂»¡øµƒ£¨º¥Öf(xi®¶)◊Éåßîµ(sh®¥)≈cœÚ¡øàˆµƒΩªìQ“ª÷¬����°£‘⁄þ@∑N«Èõrœ¬����£¨¬ì(li®¢n)Ωj(lu®∞)æÕ «Levi-Civita¬ì(li®¢n)Ωj(lu®∞)£¨À¸ «¿Ë¬¸¡˜–Œ…œŒ®“ª¥_∂®µƒ∂»¡ø¬ì(li®¢n)Ωj(lu®∞)���°£
Õ¨ò”����£¨Œ“ÇÉ”√“◊∂Ƶƒ’Z—‘√Ë ˆìœ¬ µƒé◊∫Œ“‚¡x��°����£ø’¸c“ª¸cO”–É…ÇÄ ∏¡ø∑÷ÑeûÈOQ∫ÕOQ'°£OQ—ÿ÷¯OQ'µƒ∑ΩœÚ∆Ω“∆µΩQ’¸c��£¨µ√µΩ ∏¡øO'P'£ªOQ'—ÿ÷¯OQµƒ∑ΩœÚ∆Ω“∆µΩQ¸c�£¨µ√µΩ ∏¡øOP°£»Áπ˚ø’Èg≤ª¥Ê‘⁄윬 ����£¨ƒ«√¥P¸c∫ÕP'¸c÷ÿ∫œ£ª»Áπ˚ø’Èg¥Ê‘⁄윬 �����£¨ÑtÉ…¸c≤ª÷ÿ∫œ���£¨±ÿÌö∏Ωº”“ªÇÄ“∆Ñ”≤≈ï˛÷ÿ∫œ��°£∂¯þ@ÇÄ∏Ωº”µƒ“∆Ñ”���£¨æÕ «ìœ¬ £®≈§«˙£©µƒé◊∫Œ–ßë™°£
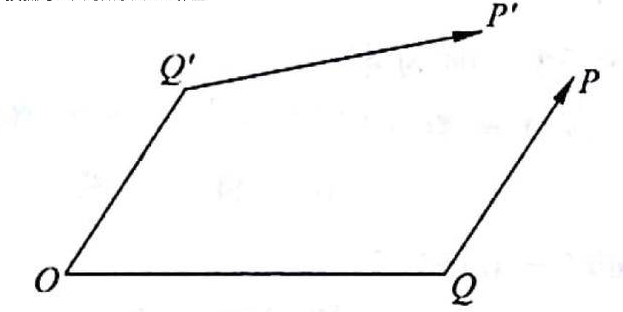
‘⁄ŒÔ¿Ì…œ�£¨ìœ¬ èà¡øø…“‘√Ë ˆïrø’÷–¥Ê‘⁄µƒ◊‘–˝-◊‘–˝œýª•◊˜”√ªÚ◊‘–˝-Ð⵿œýª•◊˜”√£¨À¸ÇÉï˛ πµ√ïrø’Æa(ch®£n)…˙≈§«˙��°£¿˝»Á���£¨‘⁄ꀓÚÀπÃπ-ø®ÝñÃπ¿Ì’ì÷–����£¨“˝¡¶àˆ∑Ω≥Ã∞¸∫¨¡À윬 èà¡ø◊˜ûÈ“ªÇÄ‘¥Ìó£¨À¸∑¥”≥¡ÀŒÔŸ|(zh®¨)µƒ◊‘–˝√Ð∂»��°£‘⁄þ@∑N¿Ì’ì÷–�£¨ïrø’≤ªÉH”–èù«˙£¨þÄ”–≈§«˙�°£


 ø∆åWÃΩÀ˜2024-10-07
ø∆åWÃΩÀ˜2024-10-07